Esquema Combinatório ¶
O esquema de esquecimento de dados do BRF pode ser compreendido com o auxílio de uma estrutura de dados chamada heap binomial. Na verdade, estas propriedades e semelhanças entre o BRF e as Heaps Binomiais foram descobertas muito depois da criação do esquema, "acidentalmente". A implementação do BRF não faz referência a esta teoria, apesar de seu fundamento matemático ser a base do funcionamento do BRF como esperado.
Uma heap binomial é definida como um conjunto de árvores binomiais, então vamos introduzir primeiramente o conceito das árvores.
Árvores Binomiais ¶
São árvores ordenadas, onde os filhos de cada nó aparecem da esquerda para a direita em ordem decrescente de grau, e podem ser definidas recursivamente da seguinte maneira:
- B0 = árvore binomial de ordem 0, com somente 1 nó;
- Bk = árvore binomial de ordem k, obtida anexando-se à raiz de uma árvore Bk-1 uma outra árvore binomial Bk-1. A raiz de uma das árvores Bk-1 é escolhida para ser a raiz da árvore BK. Em seguida, a raiz da outra árvore é acoplada como filha da primeira, se tornando então sub-árvore da nova árvore.
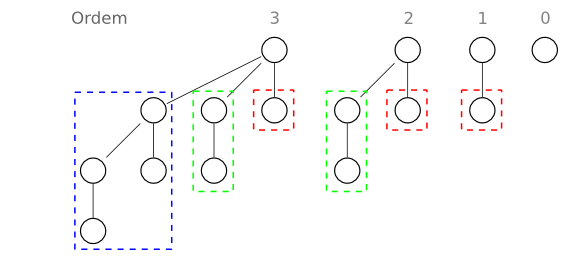
A figura abaixo apresenta árvores binomiais de ordem 0 a 3. A raiz de uma árvore Bk tem k sub-árvores Bi onde 0<=i<=k-1. Por exemplo, a árvore binomial de ordem 3 é ligada às árvores de ordem 2, 1 e 0 (destacadas em azul, verde e vermelho respectivamente).
Propriedades ¶
Uma árvore binomial de ordem k (Bk) tem as seguintes propriedades:
- Possui 2k nós;
- A altura da árvore é k;
- Existem Ck,i nós na profundidade i, sendo i=0,1,...k;
- A raiz tem grau k e é o nó com maior grau da árvore;
- Considerando os filhos da rais da esquerda para a direita com índices k-1,k-2,...,0, cada filho i é raiz de uma sub-árvore Bi.
Indexação dos vértices ¶
Consideraremos no nosso trabalho uma indexação de vértices como numa pesquisa em profundidade com atribuição de índices no momento de desativação dos vértices. Ou seja, um vértice é rotulado no retorno da busca, no momento em que todos os seus descendentes já tiverem sido processados.
[inserir figura - exemplo de árvore indexada]
Operação de união ¶
Considerando a indexação que descrevemos acima, precisamos analisar como os índices são ajustados numa operação de união.
A união acontece sempre com duas árvores de mesma ordem k. Visto que ambas as árvores possuem 2k vértices, queremos uma nova indexação que considere os 2k+1 vértices. Sugerimos então que após a escolha da raiz de uma das árvores de ordem k (Bk) como raiz de Bk+1, todos os seus vértices sejam re-indexados no intervalo [2k+1,2k+1] e a outra árvore de ordem k (bk) seja anexada como sub-árvore mais a esquerda de Bk (com seus 2k vértices), compondo assim a árvore Bk+1.
Vejamos um procedimento para tal re-indexação:
for v in B_k: index[v] = index[v] + 2^k pai[raiz[b_k]] = raiz[B_k] raiz[B_k+1] = raiz[B_k]
[inserir figura - exemplo de união]
Relação pai-filho numa árvore binomial ¶
Segundo o Teorema Fundamental da Aritmética, todo número natural maior do que um possui uma fatoração canônica única, que é sua decomposição em fatores de números primos. Já que 2 é o único número primo par, podemos enxergar a fatoração como uma potência de 2 seguida por potências de números ímpares. Considere o valor impar como o produto de todos os fatores ímpares.
A relação de parentesco entre os vértices pode ser definida da seguinte maneira:
(I) Seja n = 2^p^*impar, pai[n] = 2^p^*(impar+1).
Prova (esboço) ¶
Para verificar a correção da afirmação acima, vamos verificar as de atribuição de índices do procedimento de re-indexação proposto acima.
Base: União de duas árvores B0
Existe apenas um nó em cada árvore, ambos com índice 1. A raiz da árvore B0 é escolhida para ser a raiz de B1. O vértice de B0 receberá o novo índice 1 + 20 = 2. A raiz de B0 se torna pai da raiz de b0 e a raiz B0 se torna raiz de B1.
Hipóstese indutiva: Propriedade válida para Bk
Passo indutivo: Verificar a validade para Bk+1
Temos então duas árvores de ordem k onde a relação de parentesco (I) é válida. A árvore bk não terá seus índices alterados, portanto a propriedade se mantém. Para os vértices em Bk temos as seguiintes possibilidades, de acordo com sua localização na árvores:
- Raiz A raiz não tem pai, então a propriedade não se aplica;
- Nós internos Diante do fato que todos os índices são acrescidos do valor 2k, precisamos provar o seguinte:
Se pai[2p*impar] = 2p*(impar+1), então pai[2p*impar + 2k] = 2p*(impar+1) + 2k.
---
- n=2p
No caso de n ser uma potência de 2, podemos obter os filhos de n através do seguinte procedimento:
for i in [1..p]: filho[n][i] = 2^p-i^*(2^i^-1)
Vejamos o exemplo para n=16 (p=4):
filho[16][1] = 2^4-1^*(2^1^-1) = 8 filho[16][2] = 2^4-2^*(2^2^-1) = 12 filho[16][3] = 2^4-3^*(2^3^-1) = 14 filho[16][4] = 2^4-4^*(2^4^-1) = 15
Perceba que o fator (2i-1) é o valor de impar na fatoração de cada filho de n. Então, partindo da fatoração dos filhos, se adicionarmos 1 ao valor de impar chegaremos a 2p-i*(2i) = 2p, que é exatamente o valor de n. Portanto, vale a propriedade (I).
---
A tabela abaixo apresenta a fatoração dos números de 1 a 20 e os valores encontrados para p e impar, possibilitando o cálculo do pai do vértice n na heap.
| Vértices | Fatoração | p | 2p | impar | pai |
| 1 | 20*11 | 0 | 1 | 1 | 2 |
| 2 | 21*11 | 1 | 2 | 1 | 4 |
| 3 | 20*31 | 0 | 1 | 3 | 4 |
| 4 | 22*11 | 2 | 4 | 1 | 8 |
| 5 | 20*51 | 0 | 1 | 5 | 6 |
| 6 | 21*31 | 1 | 2 | 3 | 8 |
| 7 | 20*71 | 0 | 1 | 7 | 8 |
| 8 | 23*11 | 3 | 8 | 1 | 16 |
| 9 | 20*32 | 0 | 1 | 9 | 10 |
| 10 | 21*51 | 1 | 2 | 5 | 12 |
| 11 | 20*111 | 0 | 1 | 11 | 12 |
| 12 | 22*31 | 2 | 4 | 3 | 16 |
| 13 | 20*131 | 0 | 1 | 13 | 14 |
| 14 | 21*71 | 1 | 2 | 7 | 16 |
| 15 | 20*151 | 0 | 1 | 15 | 16 |
| 16 | 24*11 | 4 | 16 | 1 | 32 |
| 17 | 20*171 | 0 | 1 | 17 | 18 |
| 18 | 21*32 | 1 | 2 | 9 | 20 |
| 19 | 20*191 | 0 | 1 | 19 | 20 |
| 20 | 22*51 | 2 | 4 | 5 | 24 |
Heap Binomial ¶
Uma heap binomial é uma floresta composta por árvores binomiais que satisfaz às seguintes propriedades:
- Cada árvore da floresta é uma heap (de mínimo ou de máximo);
- Não contém mais do que uma árvore binomial de mesma ordem k.
Para manutenção desta segunda propriedade das heaps binomiais, utiliza-se a operação de união. Sempre que surgirem duas árvores de mesma ordem k, elas devem ser unidas formando uma nova árvore de ordem k+1. Na união de duas árvores, deve-se considerar a chave das raízes para definir qual será a nova raiz (garantindo a preservação da propriedade 1 das heaps binomiais). As operações de união devem acontecer ordem a ordem, começando pela ordem mais baixa com ocorrência de mais de uma árvore, e devem se repetir até que só haja uma árvore binomial de cada ordem.
Propriedades da política logarítmica do BRF ¶
A conhecimento de heaps binomiais facilita o entendimento da transição dos arquivos no BRF ao longo do tempo. Considere que existe uma heap para cada arquivo.
O BRF se comporta num modelo de "Espelho com Incrmentais Reversos". Portanto o último backup completo (espelho) é armazenado num sistema de arquivos em separado, e cada vez que uma cópia sair do backup ela deve entrar na heap (volumes incrementais reversos). O nó que receberá tal versão do arquivo tem índice igual à etapa do BRF. Nas etapas seguintes, esta versão pode se movimentar ou não na heap, a depender da entrada de outras versões no esquema.
Lista de nós preservados na etapa n ¶
A fim de controlar o espaço ocupado pelo backup, o BRF reutiliza o espaço já alocado, como num esquema de rotação de dispositivos que armazenam backups. Na política logarítmica, após n etapas o BRF tem |_log n_| volumes de dados. Considerando o sistema de arquivos como uma heap, ele preserva o nó mais recente de cada ordem, entre 0 e |_log n_|).
[inserir figura - intervalos de ativação]
| Etapas | B0 | B1 | B2 | B3 | B4 | B5 |
| 1 | 1 | |||||
| 2 | 1 | 2 | ||||
| 3 | 3 | 2 | ||||
| 4 | 3 | 2 | 4 | |||
| 5 | 5 | 2 | 4 | |||
| 6 | 5 | 6 | 4 | |||
| 7 | 7 | 6 | 4 | |||
| 8 | 7 | 6 | 4 | 8 | ||
| 9 | 9 | 6 | 4 | 8 | ||
| 10 | 9 | 10 | 4 | 8 | ||
| 11 | 11 | 10 | 4 | 8 | ||
| 12 | 11 | 10 | 12 | 8 | ||
| 13 | 13 | 10 | 12 | 8 | ||
| 14 | 13 | 14 | 12 | 8 | ||
| 15 | 15 | 14 | 12 | 8 | ||
| 16 | 15 | 14 | 12 | 8 | 16 | |
| 17 | 17 | 14 | 12 | 8 | 16 | |
| 18 | 17 | 18 | 12 | 8 | 16 | |
| 19 | 19 | 18 | 12 | 8 | 16 | |
| 20 | 19 | 18 | 20 | 8 | 16 | |
| 21 | 21 | 18 | 20 | 8 | 16 | |
| 22 | 21 | 22 | 20 | 8 | 16 | |
| 23 | 23 | 22 | 20 | 8 | 16 | |
| 24 | 23 | 22 | 20 | 24 | 16 | |
| 25 | 25 | 22 | 20 | 24 | 16 | |
| 26 | 25 | 26 | 20 | 24 | 16 | |
| 27 | 27 | 26 | 20 | 24 | 16 | |
| 28 | 27 | 26 | 28 | 24 | 16 | |
| 29 | 29 | 26 | 28 | 24 | 16 | |
| 30 | 29 | 30 | 28 | 24 | 16 | |
| 31 | 31 | 30 | 28 | 24 | 16 | |
| 32 | 31 | 30 | 28 | 24 | 16 | 32 |
Transição de arquivos na heap ¶
Quando ocorre a reutilização de determinado volume de backup, os dados lá armazenados são descartados. O BRF precisa garantir então que este volume não contenha a última versão de nenhum arquivo, para manter a validade do esquema.
A cada etapa do backup, um novo nó é inserido à heap, e os arquivos que não tiveram uma nova versão na heap precisam ter suas últimas versões "salvas". Assim que possível elas são então promovidas dos antigos nós para o que acabou de entrar na heap. A promoção só acontece entre nós pai e filho, nas operações de união.
Logs de modificação de um arquivo ¶
- dada uma sequência de 0's e 1's representando o log de modificações do arquivo, perguntamos: quais versões do arquivo estão preservadas?
- dois arquivos que entram na heap em etapas diferentes e têm o mesmo log de modificações têm o mesmo "destino" na heap? - tomara que sim, queremos que isso não dependa de n e sim do log
- que informações conseguimos extrair da palavra sem percorrê-la completamente, conhecendo apenas alguns aspectos dela, como quando aparece o primeiro 1, quantos 1's ela tem, ...
(trabalho em construção...)